畢氏定理速解法

話我們的行銷老師是數學高手，過去曾是補教名師，月入四五十萬。曾經在補習班嗆聲學生：從小學到大學的數學範圍只要能問倒他就有10萬元獎金。

這禮拜他小露幾手，教我們5字尾數字平方速解法及畢氏定理速解法。

畢氏定理速解法：

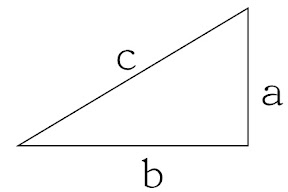
一般所知畢氏定理是指直角三角形三邊長度的關係，如上圖所示。a及b又稱作「股」，c又稱作「斜邊」。他們之間的關係是c²＝a²＋b²。有趣的是，當以「短股」為基準來看斜邊和長股，他們之間竟然存在一些有趣的規律，不過當短股數字是1和2時則有例外。

當短股是奇數時，短股的平方是長股與斜邊之和，且長股與斜邊的差是1；當短股是偶數時，短股平方的一半是長股與斜邊之和，且長股與斜邊的差是2。

運作此方法，你可僅以短股來算出直角三角形的另二邊長度。

例如當你以短股3來計算，因為是奇數，所以短股平方是長股與斜邊之和，也就是9，而且此時長股與斜邊相差1，所以9＋1除以2就是斜邊，9-1/2就是長股。

當你以短股6來計算，因為是偶數，所以短股平方的一半就是長股與斜邊之和，也就是18，而且此時長股與斜邊相差2，所以18＋2除以2為斜邊，18-2除以2為長股。特別的是當以短股為4來計算，所得的長股竟比短股要短(為3)。

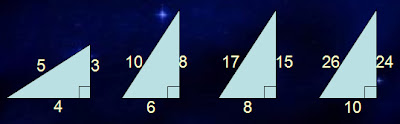
再次提醒：最大限制除前述短股數字為1時之例外之外，本法僅能以整數數字來計算。